INTRODUCTION
Mathematical sequences are ordered sets of numbers —well,
usually— which may be finite or infinite.
Sequences of numbers may be bounded (from below or above), monotonic
increasing or decreasing.
They may be convergent, divergent or oscillatory.
These are all properties of number sequences which do, however, not
name the sequences themselves.
It may be argued, that there is no need for such naming, since it is
the definition of the manner in which the elements follow one another which
matters, or the explicit rule for calculating their numbers by means of a
formula in which only the letter n occurs with or without one or
more constants.
Strictly speaking, this is true, just as there is no need to give names to
the chemical elements in the periodic table, but also these chemical
elements have names which makes speaking about them easier.
And, while the names of atoms are not substantive at all, those of
molecules are, whether or not in addition to some traditional name.
Names may, indeed, be useless and appeal to feelings which are little
scientific (if not antiscientific), but good, clear names can and should
stress structure and enhance structural thinking in a disciplinary field
of study.
There is an essential difference between defining a sequence of
numbers and developing a formula for the calculation of its numbers.
(I will return to this issue below.)
But both the definition and the calculation make use of one or more
mathematical operations, unless the values of the terms in the sequence
happen to be utterly random, which is not the type of 'ordering'
i* will be concerned with
here.
Hence, it should at least be possible to call sequences after the type of
mathematical operation used to form them.
But constants and indices can be important too, and the number with which
a sequence starts.
They all provide the material for substantive sequence names.
I will use these names in a number of articles in the present folder of
mathematical notes and papers.
Instead of having to explain them every time again, i hope this article
will suffice and save me and the reader space and time.
ADDITION, MULTIPLICATION AND EXPONENTIATION SEQUENCES
The mathematical operations on the lower levels of iteration are
addition on the zeroth level, iterated or 'systematically repeated'
addition, that is, multiplication, on the first level and iterated
multiplication, that is, exponentiation, on the second level with their
inverses.
If O is the operation, then sequences can be created on the basis of
the formula xn+1=O(xn).
In my general, substantive terminology for sequences i shall speak of
"addition", "multiplication" and "exponentiation
sequences" dependent on the type of mathematical operation necessary to
obtain a new term from one or more previous terms.
The pivot of an addition sequence is the addend (or 'summand'); the
pivot of a multiplication sequence the factor; and the pivot of an
exponentiation sequence the power.
Traditionally an addition sequence is called "an arithmetic sequence" and
the addend "the common difference"; the multiplication sequence is called
"a geometric sequence" and the factor "the common ratio".
But there it stops: in this terminology there is no notion of a
theoretically unlimited number of levels of iteration for mathematical
operations.
The use of arithmetic and geometric in this context is also
awkward.
In a sense an exponentiation sequence is more 'geometric' than a
multiplication sequence, if we associate addition with one-dimensional,
multiplication with two-dimensional and exponentiation with
three-dimensional space (or any space with three or more dimensions).
Moreover, the terms common difference and ratio are not given
from a definitional point of view but rather from the point of view of
someone who tries to find the regularity in the sequence after it has been
created.
The addend may simply be 1, it may also be the number before the previous
number, or something more complicated for which it makes little sense to
speak of "the addend".
An 'addend-a sequence' is an addition sequence of which the
addend is a.
For example, the sequence 1, 2, 3, 4, ... of natural numbers is an addend-1
addition sequence defined by
xn+1=xn+1, n≥1 and
x1=1.
The formula xn=n amounts to the same in calculations, but
is not a definition formula.
The sequence 2, 4, 6, ... of even natural numbers is an
addend-2 sequence defined by
xn+1=xn+2,
n≥1 and x1=2.
The calculation formula xn=2n amounts to the same.
A 'factor-f sequence' is a multiplication sequence of which
the factor is f.
For example, the sequence 1, 2, 4, 8, ... is a factor-2 multiplication
sequence defined by
xn+1=2·xn, n≥1
and x1=1, the sequence 1, 3, 9, 27, ... a factor-3
multiplication sequence defined by
xn+1=3·xn, n≥1
and x1=1.
The calculation formulas are
xn=½·2n and
xn=⅓·3n respectively.
A 'power-p sequence' is an exponentiation sequence
of which the power is p.
A power-2 exponentiation sequence is 2, 4, 16, 256, ... defined by
xn+1=(xn)2,
n≥1 and x1=2,
but also 3, 9, 81, 6561, ... defined by
xn+1=(xn)2,
n≥1 and x1=3.
Here the calculation formulas are
xn=(√2)2n and
xn=(√3)2n.
Of course, it is not necessary to use the terms addend and
addition, or factor and multiplication, or
power and exponentiation, in combination with each other.
Thus, an 'addend-a addition sequence' is an 'addend-a
sequence', but on the other hand, the use of the phrase addition
sequence, and similarly, multiplication and exponentiation
sequence does not require the specification of the addend, factor or
power.
Now, this terminology may be substantive and much more general than any
traditional terminology, it certainly is not universal!
In universal terms we would not speak of "addition", "multiplication" and
"exponentiation" and stop there; in universal terms we would at least refer to
the level of iteration, a level which may also be 3, 4, 5 or more
instead of 0, 1 or 2.
Such a terminology requires a system in which addition, multiplication and
exponentiation are first universalized.
And such a universal system is precisely what i offer in my paper
The Chong Operators — a universalization
in arithmetic.
The 'chong system' introduces a new symbol for a sequence, not of
numbers this time, but of operators.
This symbol for iterative operators is the character 重 (with HTML Unicode
重) for the Putonghua-Chinese word chóng in the sense of
(to) repeat, again and re-.
An arithmetic operation on the l-th level of iteration is
described by means of 重 with l, the level number, on top
of it:
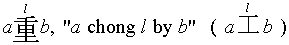
CHONG SYMBOL, WITH EXPRESSION IN WORDS (AND IN
INFORMAL HANDWRITING)
The correspondence between the new terms in the universal system of chong
operations and operators on the one hand and the old, 'specific', that is,
nonuniversalized, terms on the other is as follows:
| UNIVERSAL TERMS |
|
SPECIFIC TERMS |
| chong-(+0)/-0 operation, functor |
|
addition, addend |
| chong-(-0) operation, functor |
|
subtraction, subtrahend |
| chong-(+1)/-1 operation, functor |
|
multiplication, factor |
| chong-(-1) operation, functor |
|
division, divisor |
| chong-(+2)/-2 operation, functor |
|
exponentiation, power |
| chong-(-2) operation, functor |
|
evolution, root |
| chong-(+3)/-3 operation, functor |
|
— |
| chong-(-3) operation, functor |
|
— |
| chong-(+4)/-4 operation, functor |
|
— |
| chong-(-4) operation, functor |
|
— |
|
Note: a chong-(+l) or chong-plus functor may, just like a
chong-(-l) or chong-minus functor, be positive, 0 or negative.
A positive functor is a chong-plus or chong-minus functor which is
positive, a negative functor a chong-plus or chong-minus functor
which is negative.
|
The specific term addition converts into the universal term
chong-(+0) or chong-0 operation, the specific term addend
into the universal term chong-(+0) or chong-0 functor, et cetera.
The correspondences for the names of the lower-level sequences of numbers
are therefore:
| UNIVERSAL NAME |
|
SPECIFIC NAME |
| functor-f chong-(+)0 sequence |
|
addend-f (addition) sequence |
| functor-f chong-(+)1 sequence |
|
factor-f (multiplication) sequence |
| functor-f chong-(+)2 sequence |
|
power-f (exponentiation) sequence |
| functor-f chong-(+)3 sequence |
|
— |
For further details with regard to the chong system i refer to the special
document about the chong operators again.
In that work you will not only find formal definitions and proofs, but also
examples of
chong-3 and
chong-4 sequences with their first four
members.
You will notice that the chong-3 sequences occur in a chong-4, and the
chong-4 sequences in a chong-5 table, something that is due to the
difference between definition and calculation.
The difference i draw between definition and calculation
formulas is not at all unimportant, because they contain mathematical
operations on different levels of iteration: in general, addition,
multiplication and exponentiation in the definition formulas become
multiplication, exponentiation and iterated exponentiation in the
calculation formulas.
But the calculation formulas give a description from an improper position,
for on the level of addition multiplication does not (yet) exist.
Addition may be 'native' to one-dimensional space, on a geometrically
inspired assumption multiplication is not.
On the level of multiplication both addition and multiplication exist, but
exponentiation not (yet).
Multiplication may be 'native' to two-dimensional space, on the same
assumption exponentiation is not.
Definition formulas have meaning but are of little practical use, whereas
calculation formulas are of practical use but have little meaning.
In order to understand that the powers of 2, 3 and so on form
multiplication and not exponentiation sequences we just have to look at the
definition formulas of these sequences, which do not contain powers.
(Note that the calculation formula of the sequence 1, 2, 4, ... is
xn=½·2n, which is the same
as
xn=2n-1 with n≥1, but not the
same as xn=2n with n≥0.)
A-B-C SEQUENCES AND HEAD-H TAIL-T
SEQUENCES
I shall also name number sequences after the three terms with the indices
1, 2 and 3.
Sequences may start with a term which receives the index n=0 or the
index n=1, dependent on the role n=0 plays in digital cycles, a role which
is, perhaps, different for different (types of) cycles.
(The terminology of cycles in sequences will be discussed below.)
So, the numbers i will use for the naming may or may not be preceded by a
number with index 0.
Thus, the simplest addend-2 addition sequences are the 2-4-6 sequence
(0,) 2, 4, 6, 8, ... and the 1-3-5 sequence 1, 3, 5, 7, ... .
The simplest factor-2 multiplication sequences are (after the 0-0-0
sequence) the 1-2-4 sequence 1, 2, 4, 8, ..., and the 3-6-12 sequence
3, 6, 12, 24, ... .
The simplest power-3 exponentiation sequence (after the 1-1-1 sequence) is
the 2-8-512 sequence 2, 8, 512, 134217728, ... .
The naming of sequences so far can be made 'watertight' for sequences which
are not too complicated by adding a reference to the first term, which i
shall call "the head of the sequence", and the last term, which i shall
call "its tail", provided, of course, that such a first and/or last term
exist.
The first term is then really the first term, regardless of its index (1 or
0).
A 'head-h sequence' is a sequence which starts, or is made to
start, with the term h, a 'tail-t sequence' a sequence
which ends, or is made to end, with the term t.
Hence, the head-0 1-2-3 sequence is the sequence 0, 1, 2, 3, 4, ... of
nonnegative integers.
The head-2 2-4-8 sequence is the sequence 2, 4, 8, 16, ..., and not the
sequence 1, 2, 4, 8, 16, ... .
A head-2 tail-6 2-4-6 sequence is a set of the numbers 2, 4 and 6 in that
order.
It is more interesting that very large finite or infinite sequences can now
be given full substantive names which can be quite short, certainly in
comparison with the numbers they may contain.
Thus, the head-14 factor-4 sequence must be the sequence 14, 56, 214, 856,
3424, ..., and the head-3 power-3 sequence is nothing else than the
sequence 3, 27, 19683, 7625597484987, ... .
DIGITAL CYCLES AND THEIR NAMING
Sequences of the type i have studied do not have whole number cycles
in that exactly the same number reappears after a fixed loop length, but
they usually (or always?) do have digital cycles in that one or more
initial or final digits steadily return after a certain number of terms.
Moreover, in these sequence cycles the digits may not be evenly
distributed, all dependent on the numeral system used.
The binary system (with base 2), the ternary system (with base 3), the
quaternary system (with base 4), the quinary system (with base 5), the
system (with base 6), the octal system (with base 8) and the denary system
(with base 10) may all tell a different cyclical story about the sequence.
I will call a cycle with d digits recurring at the end of the
numbers in a sequence "a final d-digit cycle".
Similarly, i will call a cycle with d digits recurring at the
beginning of the numbers "an initial d-digit cycle".
Final one-or-more-digit cycles in the true sense of the word exist in
abundance, but it is much harder to come across an initial
one-or-more-digit cycle in which two or more different digits
continue reappearing until infinity, that is, a q-term
initial d-digit cycle for which q≥2.
(All positive integers start with 1 in binary notation, but in such
a one-term initial cycle with the length of one digit only it is the same
digit which is being repeated all the time.)
In the binary system the numbers of a sequence may turn out to develop a
very regular, in principle infinite, hierarchy of smaller cycles with fewer
final digits within larger cycles with more final digits.
An example of such a sequence is the 0-5-10 addend-5 sequence, which
contains 0, 5 and multiples of 5.
(On the basis of these multiples one could be seduced into believing it to
be a head-0 5-10-15 sequence, in which the number 5 receives the index 1.
Nonetheless, it is an addition sequence whose definition formula
does not allow of any form of multiplication.)
If we confine ourselves to the first sixteen terms here the denary notation
of the numbers does not contain more than a two-term final one-digit cycle.
What we see in the binary notation is much more interesting
tho**:
| THE 0-5-10 SEQUENCE IN
TWO NUMERAL SYSTEMS |
| N |
|
BASE 10 |
|
BASE 2 |
|
N |
|
BASE 10 |
|
BASE 2 |
| 1 |
|
0 |
|
0 |
|
9 |
|
40 |
|
101000 |
| 2 |
|
5 |
|
101 |
|
10 |
|
45 |
|
101101 |
| 3 |
|
10 |
|
1010 |
|
11 |
|
50 |
|
110010 |
| 4 |
|
15 |
|
1111 |
|
12 |
|
55 |
|
110111 |
| 5 |
|
20 |
|
10100 |
|
13 |
|
60 |
|
111100 |
| 6 |
|
25 |
|
11001 |
|
14 |
|
65 |
|
1000001 |
| 7 |
|
30 |
|
11110 |
|
15 |
|
70 |
|
1000110 |
| 8 |
|
35 |
|
100011 |
|
16 |
|
75 |
|
1001011 |
|
Note: the sets of two, four and eight numbers between horizontal lines with
their last one, two or three digits in red denote full second final
one-, two- and three-digit cycles.
|
In the base-2 head-0 addend-5 sequence the smallest final cycle is the
two-term one-digit cycle in which the the pattern (0)(1) is repeated
to infinity.
But two of these cycles constitute a new four-term two-digit cycle in
which the pattern (00)(01)(10)(11) is repeated.
Two of these higher-level cycles constitute, in turn, a new eight-term
three-digit cycle in which the pattern
(000)(101)(010)(111)(100)(001)(110)(011) is repeated.
And one may be sure that the sixteen numbers shown will together be part of
a sixteen-term four-digit cycle, which is not shown in the above table,
because it is always second cycles of a type which i will show.
(As long as you are in the first occurrence of a cycle, you cannot be aware
of being in a cycle.
That awareness does not start until after the second occurrence of the
cycle, and even then it is not proof of the existence of a cycle, let alone
of an infinite one.)
The one-term initial one-digit cycle in positive numbers in binary notation
is not the most surprising cycle one can think of.
Therefore, i will conclude with five different notations for the numbers of
the head-1 factor-2 sequence or the 1-2-4 multiplication sequence.
(Calculationwise these numbers are the powers of 2, which is why one may
be inclined to choose the exponent for the index, starting with 0.
But, again, the definition of a multiplication sequence does not allow of
exponentiation.)
All final digital cycles until the twenty-first term are simple one-digit
cycles of one, two, three or four terms long.
They are obvious and can be easily proved.
So, let us have a look at the initial digital cycles in this table:
THE 1-2-4 MULTIPLICATION
SEQUENCE
IN FIVE DIFFERENT NUMERAL SYSTEMS |
| N |
|
BASE-10 |
|
BASE-8 |
|
BASE-6 |
|
BASE-4 |
|
BASE-3 |
| 1 |
|
1 |
|
1 |
|
1 |
|
1 |
|
1 |
| 2 |
|
2 |
|
2 |
|
2 |
|
2 |
|
2 |
| 3 |
|
4 |
|
4 |
|
4 |
|
10 |
|
11 |
| 4 |
|
8 |
|
10 |
|
12 |
|
20 |
|
22 |
| 5 |
|
16 |
|
20 |
|
24 |
|
100 |
|
121 |
| 6 |
|
32 |
|
40 |
|
52 |
|
200 |
|
1012 |
| 7 |
|
64 |
|
100 |
|
144 |
|
1000 |
|
2101 |
| 8 |
|
128 |
|
200 |
|
332 |
|
2000 |
|
11202 |
| 9 |
|
256 |
|
400 |
|
1104 |
|
10000 |
|
100111 |
| 10 |
|
512 |
|
1000 |
|
2212 |
|
20000 |
|
200222 |
| 11 |
|
1024 |
|
2000 |
|
4424 |
|
100000 |
|
1101221 |
| 12 |
|
2048 |
|
4000 |
|
13252 |
|
200000 |
|
2210212 |
| 13 |
|
4096 |
|
10000 |
|
30544 |
|
1000000 |
|
12121201 |
| 14 |
|
8192 |
|
20000 |
|
101532 |
|
2000000 |
|
102020102 |
| 15 |
|
16384 |
|
40000 |
|
203504 |
|
10000000 |
|
211110211 |
| 16 |
|
32768 |
|
100000 |
|
411412 |
|
20000000 |
|
1122221122 |
| 17 |
|
65536 |
|
200000 |
|
1223224 |
|
100000000 |
|
10022220021 |
| 18 |
|
131072 |
|
400000 |
|
2450452 |
|
200000000 |
|
20122210112 |
| 19 |
|
262144 |
|
1000000 |
|
5341344 |
|
1000000000 |
|
111022121001 |
| 20 |
|
524288 |
|
2000000 |
|
15123132 |
|
2000000000 |
|
222122012002 |
| 21 |
|
1048576 |
|
4000000 |
|
34250304 |
|
10000000000 |
|
1222021101011 |
|
Note: the one-term final one-digit cycles in the base-4 and base-8
notations are not indicated separately (by means of horizontal lines
and a red color), since showing the second of these cycles would
interfere with showing the second of their two- and three-term
initial one-digit cycles.
The beginning of what seems to be a second initial digital cycle in
the base-6 numbers from the 14th term is marked with a dotted line
and first digits in blue.
|
As far as the base-4 and base-8 notations are concerned, the simplicity of
their final digital cycles is reflected in the simplicity of their initial
digital cycles, and also these initial cycles can be easily proved.
In the base-6 notation not any full initial cycle in the strict sense can
be recognized, altho the first digits from n=1 to n=8 are
repeated from n=14 to n=21.
This could mean that there is a first-digit cycle from n=1 to
n=13 which is repeated from n=14 to n=26, but even for
that preliminary conclusion the table does not provide enough information.
In the base-3 and base-10 notations, however, we can certainly detect
initial digital cycles within the confines of the table.
All first digits of the ternary numbers from n=1 to n=8 are
repeated from n=9 to n=16, and the first digits of the
numbers from n=17 to n=21 are the first digits of the same
cycle again.
The first digits of the denary numbers from n=1 to n=10 are
repeated from n=11 to n=20, and the first digit of the
number with the index n=21 is, similarly, the first digit of the
same cycle.
And yet, i can tell you that at least the initial digital cycle of the
base-10 1-2-4 sequence will turn out to not be a cycle in the strict sense
of the word when we increase n sufficiently.
There will be variations, albeit small, which will force me to speak of
"paracycles" in such a case.
By small i mean that the one or more variations must be between
'adjacent digits': 1 may change into 2, 2 may change
into 3, ... and the last available digit (9 in the denary
system) may change into 1.
Before you conclude that 'the powers of 2' have an initial paracycle of ten
terms long in their denary representation, i hasten to add that the length
of that paracycle will turn out to be much longer when you also make the
beginning of the sequence to be studied much longer.
Here, i will not go into this matter anymore, for the basic principal
purpose of this paper was the introduction and explanation of the
terminology i will use for number sequences and their cycles.
For a more detailed discussion of sequences, cycles, numeral systems and
the frequency distribution of first digits i refer to the respective
mathematical notes and papers.
67.LNW-CEN
| * |
The first-person singular pronoun is
spelled with a small i, as i do not consider myself a Supreme
Being or anything else of that Ilk. |
| ** |
Where there is some existing orthographical
variation preference will be given to the (more) phonematic
variant |
|